#Mod euler

[asktoppatpurgatory]

BOOOOOO Terrence is on screen. Stinky. Stinker. The stench.........

HES ALREADY DEAD AND HATLESS LEAVE HIM ALONE!!! THERES NO DEODERANT IN HELL CUT HIM SOME SLACK

[object-moodboards]

scenttray..... please (amelia x tray hfjone)

of course! - mod roboty

[andmaybegayer]

Last Monday of the Week 2024-09-09

It was Bandcamp Friday last friday so those go up front:

Listening: First up God's Country by Chat Pile which I cannot remember why I found it but is extremely noisy metal. Blunt, to the point.

A Dog A Deer A Seal by Hit Bargain has featured on a Monday before but now I actually bought the album, here's the title track. Very modern-style rock.

The Envoy by Gavlina Rayna Russom, her first solo album after leaving LCD Soundsystem, soundscape electronic and voice based on The Left Hand of Darkness.

Cyberspace Database by Fornax Void, sort of the evil mirror dimension version of Businessfunk which now that I think about it has never come up on here? Incredible. Anyway a sort of fantasy soundscape for a cyberspace environment. Huge album too, like 50 songs.

Alright back to our regularly scheduled programming

Watching: New! Dynamo! Dreams! from Ian Hubert,

This is the first time we're back at what was started in Ep1 so there is in fact some kind of plot, although the series remains supremely vibes-based. Excellent extensive rampaging robotaxi sequence. Dynamo Dreams is mostly about the props and atmosphere.

Reading: Finished The Tyrant Baru Cormorant after a brief lapse in reading. It's got problems! I really like a lot of it but it keeps on pausing the book to tell us about the blogs and wikipedia pages Seth Dickinson has been reading. Have you heard of Euler's Formula? What about the evolutionary argument for homosexuality? Yo did you hear about plants that avert scurvy? I am going to tell you about these in a boringly straightforward didactic way for the next 200 pages while occasionally progressing the plot.

Things I like: There is a very real sense of trying to balance everyone's schemes. Despite the fantasy communication techniques there's a lot of hidden information that gets used well, and the vibe of Baru's person-blindness is felt heavily but by anyone trying to make a plan run smoothly. Baru gets so messed up over the course of these books and it works to demonstrate how she's taking herself to pieces to make this work.

When Baru is actually doing her thing you can ignore the sort of awkward frankensteined nature of the world around her, but when explicit attention is drawn to it it quickly starts to fall apart, and the introduction of the Lightning Cult has me worried that this will only get more severe. Seth Dickinson seemingly cannot do Greg Egan, but they can do the rest of the Baru Cormorant pretty solidly.

Also more Skin Horse. Only to about 2012 so far.

Making: Some abortive soldering projects, hampered by my lack of good quality solder, I only have pure tin/copper blend in pretty coarse gauge, you want something finer and with a little silver for this.

Started working through some Control Theory lectures to brush up on that because I'm also working through some ROS tutorials, I want to make my robotics projects more broadly useful and integrating ROS/microROS might go a long way to helping that.

Playing: Ash and Adam's Gobsmacked, an early access roguelite arena combat goblin game that came out recently. Big focus on mobility, you can run and jump and glide around levels while taking out a bunch of robots. Still pretty finicky, controls are on the slippier side so on the plus side "high skill ceiling" but also "uncontrollable".

A touch of Minecraft, poking at Modrinth mod manager rather than my usual manual mod installation because I was unwilling to spend time figuring out how some of the new mods interact. I really do want to stick with a world long enough to do something interesting sometime.

Tools and Equipment: I set up Tailscale to link my server with my devices when they're in the field, using a headscale node running on my cloud server. It's really nice once you have all the basics sorted out, works smoothly. Worth a look if you want to securely access your home network while on the go.

[azumeliablorbobracket]

Welcome!!

Hiya! Do you like voting on other people's blorbos for your own amusement? Do you like tournaments with weird obscure characters? Do you just... like tournaments? Just in general?

Well, you can get any of those things here, with the Azumelia Blorbo Battle! Or Azumelia Blorbo Bracket, I've kind of alternated between the two names... both work fine.

Ran by me, @azumelia - as the name would imply - and consisting of characters I'm particularly fond of - as the name would also imply - this is a 16-character tournament in a double elimination format consisting of my very own, extremely specific blorbos.

It's primarily inspired by other "blorbo brackets," such as @rook-blorbo-bracket or @noodleblorbobracket, since I thought it was a fun idea, but some other tournaments that serve as inspirations (or are simply ones I like a lot) include @who-do-i-know-this-man, @overworkedblorbobattle, @best-kirby-character-tournament, @generic-man-in-suit-battle, and @obscurecharactershowdown!

Here's your bracket for Round 1! The roster in written form is under the read more cut. Voting begins... soon, probably! Maybe later today, maybe in a few days... Who knows? I've never done one of these before, I'm just kind of winging it here.

Penny (Pokemon Scarlet & Violet) vs. Penny Crygor (WarioWare)

Homura Akemi (Madoka Magica) vs. Taranza (Kirby)

Cole Brew (Rhythm Doctor) vs. Bethany (The Binding of Isaac)

Yuuri (Girls' Last Tour) vs. Kyoko (Kunio-kun / River City Girls)

Moss (Pikmin 4) vs. Hat Kid (A Hat in Time)

Annalynn Midway (Annalynn) vs. Amelia Euler (HfjONE)

Charlotte (Making Fiends) vs. Čeda Čedović (Poor 4)

Acid Rainbows (Rivals of Aether Mod) vs. Annie (Turnip Boy Commits Tax Evasion)

[favoritepinestriplet]

Wassup internet!

Decided to open a little blog on here to better reach out to clients and keep in trouch with friends, come chat with me about anything or everything. Pretty boring running the shack on some days, but someone's gotta help soos without Uncle Stan always around.

I'm Alexander Euler Pines, technically I'm the middle child of my dad's triplets but at least I'm not the one who's a stick in the mud like my brother; and people say I take after dad! Eh, I'm pretty sure I take after uncle Stan more. 'Sides, it's not illegal if you aren't caught!

OOC: Mod here! I'm the creator of this OC, @matrixbearer2024, this is Alex from my FordFamilyAU! Triplet middle child, come interact with him to annoy him or just to gossip. The triplets here are set post-weirdmageddon but depending on who I'm RPing with this could change!

[techtakesoff]

planets for a maid of light and maid of hope?

Note from Mod Dirk: This is a very long post, so I have provided a keep reading. Please leave thanks to Mod Squarewave for their amazing posts. Thank you for being patient, please enjoy!

For the Maid of Light:

The Maid of Light is a really neat title. They are full of light, and they spread light to everyone around them. It's also their role to protect that light, which they might struggle with because of how freely they share it.

Maybe someone else in their session is taking advantage of knowledge the Maid lets slip and using it against them, or the Maid themself is losing track of their own knowledge. They might be relying too much on luck and wittiness to get them out of trouble, and their carelessness is putting other people at risk.

The Maid needs to learn to pick their battles, and their quest will reflect this; they can't count on always knowing everything, or on coming up with solutions on the fly, regardless of how much they want to or how well it's worked out for them so far.

One way I can see this quest playing out is as a large puzzle with missing pieces; it takes the form of a large, central fixture on the planet that requires rune tablets to be collected from across the land and placed on an altar in some certain order.

However, the Maid eventually realizes that some of the tablets they're being told to get just don't exist, and the instructions for how to arrange them are nonsensical and contradictory. (If this session also has a Void player, they might be a lot of help in getting the Maid of Light to realize this :] )

The Maid also can't solve the puzzle just by guessing random combinations of tablets. This is endlessly frustrating to them, and it might take them a long time to finally accept that their tried-and-true methods won't work here.

The real solution might be breaking into the puzzle with brute force, or waiting for it to open on its own, or reaching a deal with the planet's denizen to have them open it. However it goes, the Maid learns the limitations of their inner Light, and also comes to understand how that Light can reveal other paths to victory.

The structure of this planet would be very bright and mystical, something appealing to the Maid and making them want to explore it thoroughly. I like the Land of Runes and Electrum as a name for this one.

"Runes," as mentioned previously, refers to magic or mystical symbols carved into the quest tablets. It also sounds similar to "ruins," as in ancient buildings for the Maid to explore. "Electrum" is a bright pale metal that was historically used to decorate the tops of pyramids and obelisks, and what the first known metal coins were made of.

It's also what the present-day Nobel Prize medal is made of; the Nobel is a symbol of knowledge and scientific or artistic achievement. LORAE would be covered in glittering metallic monuments decorated with runes, which the Maid of Light can't resist trying to decode the meaning of.

Another planet idea I really like is the Land of Knots and Crosses. This one is a pun on "noughts and crosses," another word for the game tic-tac-toe, which is easily solved once one knows the strategy.

Because it is so easily solved, people have come up with many more complicated versions of tic-tac-toe to keep challenging themselves; it's also a model game for teaching game theory to artificial intelligences.

"Knots" are a symbol of wisdom in many cultures and can be functional or decorative "puzzle knots," knots that require knowledge and persistence to tie/untie.

"Crosses" in this case refers to bridge crossings, which could form fantastical knot-like structures, and are often the subject of logic puzzles themselves, such as the many variants of the "dog, sheep, and cabbage" puzzle. There is also the famous "Seven Bridges of Königsberg" problem, which was proven to have no solution by the mathematician Euler.

For the Maid of Hope:

Like the Maid of Light, the Maid of Hope radiates their aspect everywhere they go. They are full of hope and positivity, to the point that they have a severe lack of logic and objectivity.

In their eyes, everything they do happens because they believed it would, and anything they fail at was just because they let themself down and didn't believe hard enough. They start out with a very shallow understanding of Hope, keeping the idea detached from reality and basically operating in an alternate universe of ideals.

They're walking through an imaginary maze that doesn't line up with where the walls are in the real world, basically. This could lead to them being seen as naïve or stubborn; either way the Maid of Hope needs to learn how to focus their Hope into meaningful action, even if it means compromising on some of their surface-level ideals.

An actual maze is the most clear-cut way for this quest to manifest. It could take up the whole planet or just part of it, but it's very large either way, and the walls are constantly shifting around the Maid.

Crossroads are marked with choices the Maid must make, like which of two opposing consorts they should side with, or which gate they should open with a single-use key.

To the Maid these choices seem either totally obvious or totally arbitrary, because they aren't thinking with any kind of long-term strategy. They find themself being lead in circles and losing progress, never getting any closer to the end of the maze.

It's only once the Maid slows down and takes the time to really examine the situation, weighing the pros and cons of each option, that they are able to make any headway. By the time they reach the end of the maze, the Maid has learned how to put their hopeful attitude into practice and use it to help others.

The Land of Weights and Mirrors is one possible name for this planet. "Weights" refers to the weights that balance a scale, symbolizing practicality and justice in the Maid's choices, and also to the metaphorical "weight" of their consequences, as the Maid must take responsibility for their actions and beliefs.

"Mirrors," of course, are reflective surfaces, and the concept of a maze or "house of mirrors" isn't a new one, but I like the idea of a gallery of mirrors that all show slightly different versions of reality, not so much like "funhouse mirrors" but rather windows that allow the Maid of Hope to see things from other people's perspectives.

They are also literal "opportunities for reflection," where the Maid can look at themself and think about the choices they've made and what they have accomplished.

Other potential planets for the Maid of Hope: Land of Glass and Roses -- as in the expression "through rose-colored glasses," meaning to have an inaccurate and falsely positive perspective on something due to nostalgia;

roses and glass also symbolize frailty and are common motifs in fairytales, which present a morally-simplified view of the world Land of Thread and Ivory -- thread as in the expression "hanging by a thread," and could also refer to tapestries that show the planet's lore and the Maid's decisions as interpreted by the consorts;

ivory as in "up in your ivory tower," meaning someone who doesn't know the real state of the world and appears to have unrealistic standards of morality;

ivory is also a historical symbol of luxury that looks beautiful but comes from poached animals, representing the consequences of ideals (death and suffering as the consequence of prioritizing aesthetics)

[comp6841]

Midterm - Past Paper 2017

=== Question 0 === (3 Marks)

What is the most important property for a cryptographic hash function to have to make it as resistant as possible to birthday attacks?

.[A] Preimage resistance .[B] Collision resistance .[C] Confidentiality .[D] Symmetry .[E] Second-preimage resistance .[F] Non-determinism

The whole idea behind the “birthday paradox” is that given a room of people it “seems more likely than you think” that any two people will have the same birthday. The key part here is “any” - the idea of being able to find “any” 2 hashes for a function is a collision attack; hence the answer is B.

=== Question 1 === (3 Marks)

You are a developer of opensource fake-news software called "The trumpet shall sound", or "Trumpet" for short. You wish to use a cryptographic algorithm to generate a 64 character "digital fingerprint" of the "Trumpet" binary, which you will display on your web site so that people can check that they have downloaded a legitimate and unaltered copy of "Trumpet".

What is the most important property for this cryptographic fingerprint algorithm to have?

.[A] Preimage resistance .[B] Collision resistance .[C] Confidentiality .[D] Symmetry .[E] Second-preimage resistance .[F] Non-determinism

If someone is trying to make an illegitimate document, they are essentially trying to fake the hash which means it must be either A, B or E. Since they are looking to find another x’ (i.e. fake document) such that h(x) = h(x’) where x is the original document, the answer is clearly second-preimage resistance - E.

=== Question 2 === (3 Marks)

A MAC is designed to provide .[A] Neither Integrity nor Authentication .[B] Authentication but not Integrity .[C] Integrity but not Authentication .[D] Integrity and Authentication .[E] A Very Fashionable Device

A MAC is a hash of a message and a key - the purpose of hashing this is to ensure the data is not modified (i.e. integrity) and that the other individual knows the key (i.e. authentication) so they can verify the MAC code. Therefore the answer is clearly D.

=== Question 3 === (3 Marks)

You have a password file of 1,000 password hashes. Assuming that 50% of the passwords used were weak passwords which can be found in a dictionary of 1,000,000 common passwords, and that hashing a password takes 12 bits of work on average, roughly how many bits of work would it take to discover all these 500 or so weak passwords?

Note: only enter DIGITS in your answer (or else the automarker will mark it wrong.) _____

The easiest way to do this problem is to firstly hash all the dictionary passwords and put them in a table.

Work = 1,000,000 * 2^12 = 2^20 * 2^12 = 2^32

If you have them in a hash map, you can pretty much do an O(1) (constant time) lookup. This is comparatively very small compared to the computation required to compute a hash function, so we can ignore this. (i.e. we don’t need to worry about the 50% being weak at all here really) So the answer is 2^32 bits of work.

=== Question 4 === (3 Marks)

As for Question 3 but now assume that each password is appended to a different 32 bit number (a salt) before the hash was computed, and that the salt number for each password hash is stored, unencrypted, next to the hash in the password file.

Roughly how many bits of work would it take to discover all the 500 or so weak passwords in this case?

Note: only enter DIGITS in your answer (or else the automarker will mark it wrong.)

Now we actually have to consider the assumption that 50% of the given 1000 passwords are weak. This is actually a generalised birthday problem (except 1/2 for weak instead of 1/365 for birthdays) - i.e. given a room of 1,000 people, what is the value of n such that the probability that n people (0 <= n <= 1000) have a birthday on the same day is 0.5? I think solving this is well beyond the scope of this course - so in this question, I will make the assumption there is instead a 50% chance for any ‘given password’ to be weak. This means that on average your expectation would be that you need to check all the passwords to see if they are weak - the actual answer to the generalised birthday problem is not that far off 1,000 so I would argue we may be overestimating the amount of work by 2^0.5.

For each of the passwords we need to check, we will need to calculate the hash with the given salt for each of the common passwords. Now remember, around half of them are weak; this means on average we will only need to hash half the password list for the ones which are weak. The normal passwords we will end up wasting our time on the entire list:

So our answer based on our assumption would be 41.5 bits of work; I would argue that once you take the unintended generalised birthday problem into account it is probably closer to 41 bits of work.

=== Question 5 === (3 Marks)

Below are six lists of expenses submitted by six politicians. Sadly 3 of the politicians are dishonest and submitted made-up fake expense claims, not costs that they really incurred. :(

{{{ Albus Bert Carl Dave Egon Fred

269 6,296 543 1,137 503 206 1,428 3,217 220 638 4,195 74 3,840 520 3,080 696 5,780 257 2,163 456 5,070 543 7,774 350 165 111 108 113 986 50 2,701 2,176 8,078 145 884 426 339 476 7,963 313 6,530 3,226 64 2,607 68 236 50 108 942 824 2,457 701 9,801 94 17 10 7,952 422 5,717 17 423 112 5,332 5,723 29 158 37 13 5,705 964 3,933 609 723 9,048 8,851 750 6,122 5,769 172 295 99 7,905 91 19 498 165 6,424 9,953 89 275 5,583 3,008 48 491 19 898 56 1,396 8,339 2,675 758 506 158 19 1,945 8,212 427 3,467 1,244 238 916 897 8,503 9,217 2,445 51 3,618 392 3,617 26 866 921 4,219 941 338 1,349

}}}

Correctly identify the status of each politician.

==== 5.1 Albus ==== .[A] Honest .[B] Dishonest

==== 5.2 Bert ==== .[A] Honest .[B] Dishonest

==== 5.3 Carl ==== .[A] Honest .[B] Dishonest

==== 5.4 Dave ==== .[A] Honest .[B] Dishonest

==== 5.5 Egon ==== .[A] Honest .[B] Dishonest

==== 5.6 Fred ==== .[A] Honest .[B] Dishonest

Had to look up a bit about datasets to find out that this was utilising Benford’s law (on Wikipedia) - an observation regarding the frequency of leading digits in real-world datasets. Basically the idea is they should occur fairly closely to the distribution in the image below:

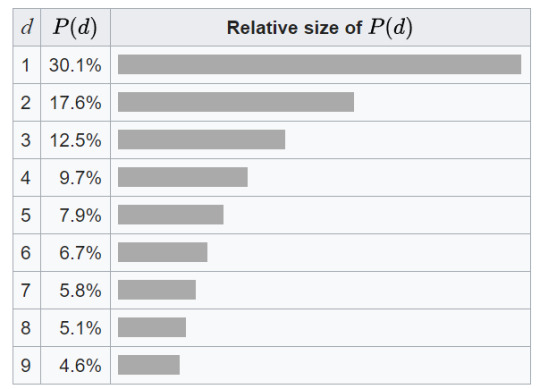
So what you need to do in the above dataset is count the number of 1′s for each of the politicians as leading digits and the percentage they represent in each column. I did this and got A - 29%, B - 33%, C - 10%, D - 14%, E - 5% and F - 24%. You can clearly see that A, B and F more closely resemble real-world data and are more likely the honest politicians (you can also check this with 2′s as well). Therefore the dishonest politicans are likely C, D and E.

=== Question 6 === (10 Marks)

What is the 5th word in the plaintext for the ciphertext below?

{{{ HHPET IAESR DTEHN SRAKA UASMI UEOYR CNWOK FNERA TRONE TNYLO SOENO OHDAS RYUSW DONUR BNSGI STLAU HTTOO DSAHE EWSYO SRTEC IFHWO EHNOC TIHGM AENUB EAERW DEYRV EYHTA OUGNS WSODE ROEVN HLTLA ESSEE SRTEC ONSDA YVREE SNIEO ENHTI IAKRD WOENN AYROA EOHTN OIYFR SAERU TNABU IIGNH RAAPN IFROK NSATN TEUBC OODUY NOKTN AWHTO CAOLT AECDK TIENB RSUBI IEFDI ETFYF NTEBE YAHTE LUBRO TNEKA YHNET EURAO ENHTI EAKRD HETNV YUHGO EURAO COATN LULAT HITNY KDRAE }}}

THEPE 

My immediate idea was that this was a transposition cipher because it would be kinda cruel otherwise since we aren’t given any word spacing information or punctuation. The first word I saw was “THE” at the start, so I figured it must mean something - I attempted assembling with key length 3 however this didn’t make sense (neither did a length of 4). When I tried a length of 5, I got “THEPH” -> “RASEI” -> “NTHED” -> "ARKAS” (i.e. “THE PHRASE IN THE DARK AS”). This seemed to make sense and checking it a bit further, this seemed to be the correct mapping which is (1,2,3,4,5) -> (5,2,4,3,1) - this means the 5th word is “DARK”.

=== Question 7 === (20 Marks)

Suppose we convert letters and other characters into numbers in the range 1..54 using the following table and then separately encipher each of these numbers using RSA with a public encryption key of 23 and a modulus of 55.

{{{ 1 <         21 L       41 4 2 >         22 M     42 5 3 ?         23 N      43 6 4 /         24 O      44 7 5 :         25 P       45 8 6 ;         26 Q      46 9 7 “         27 R      47 ( 8 '         28 S       48 ) 9 @       29 T      49 * 10 A      30 U     50 + 11 B      31 V      51 , 12 C      32 W     52 - 13 D     33 X       53 . 14 E      34 Y       54 / 15 F      35 Z 16 G     36 SPACE 17 H     37 0 18 I      38 1 19 J      39 2 20 K     40 3 }}}

For example the plaintext ":)" would be converted into 5,48, and then each of these numbers would be individually encrypted using RSA to produce the cipertext 15,42.

The remainder of this question has been encrypted using RSA with an encryption key of 23 and a modulus of 55.

{{{ 24,18,49,16,48,49,33,10, 2,12, 52,49,48,16,19,20,16,24,18, 2, 7,16,31,50,49, 7,24, 2,19,12, 16,18,10, 7,16,11,49,49,12,16, 49,12,23,48,34, 5,24,49,52,16, 50, 7, 2,12,26,16,48, 7,10,16, 43, 2,24,18,16,10,12,16,49,12, 23,48,34, 5,24, 2,19,12,16,25, 49,34,16,19,20,16,29,35,16,10, 12,52,16,10,16,33,19,52,50,21, 50, 7,16,19,20,16, 3, 3,47,16, 16,24,18,49,16,10,12, 7,43,49, 48,16,23,19,52,49,43,19,48,52, 16, 2, 7,16,53,53,53,53,53,53, 53,53. }}}

What is the answer codeword?

If you read a little about RSA you would know that you pick 2 primes (p and q) at the beginning of the algorithm which multiply together to give you your modulus. Since we have a modulus of 55, then p = 5 and q = 11. This means Euler’s totient = (5 - 1)(11 - 1) = 40. For the public key it is clear that 23 has been chosen as it doesn’t share any factors with 40. To determine the decryption key we can solve d * e (mod ϕ) = 1. We will do this via Extended Euclidean algorithm:

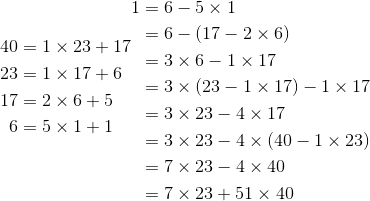
Therefore our private key is (d = 7, n = 40). We can use this to decrypt the answer if we want rather quickly; to save time you could probably just calculate the stuff near the end - for example once you calculate 53 ^ 7 (mod 55) you unlock quite a few bits of the text. An easy way to do this is to realise that 53 (mod 55) = -2 (mod 55) and -2 (mod 55) = -128 (mod 55) = 37. Anyway I got lazy and just dumped it all in a script:

So the codeword is ‘00000000′.

[seb-sec-blog]

RSA activity

This activity took me on a wild journey to make my own RSA keys. Naturally being a cyber actor I created uncrackable keys.

First, we must select 2 prime numbers, p & q. I chose 5 & 7, which we multiply together to get the number n = 35.

We then calculate Euler’s totient, which is represented by phi and given by  ϕ(n) = ( p-1 ) * ( q-1), which for us is 24.

Then we select a number e between 3 and  ϕ(n) which is relatively co-prime with  ϕ(n), that is, e doesn’t share any factors with  ϕ(n)- 17 works.

e and n now form our public key:(e=17, n=35)

We must now choose a value d that satisfies  (e * d mod ϕ = 1). Lets pick 17 since the website doesn’t seem to like large numbers. This number now completes our private key: (d=17, n=35) (pretend this isn’t also our public key, that might be a bad practice in real life)

We now have two keys we can use to encrypt and decrypt messages by doing the following: 

 c = me mod n, where c is the encrypted value of the ascii leter m, and e and n are from our public key. If we choose the letter ‘A’ (ascii value 65), we get a c value of 25.

To decrypt this, we apply a similar formula:

m = cd mod n , with d and n from our private key. Applied to a c value of 25, we get back 65=A

To summarise: We form a public key starting from two prime numbers and can use this key to encrypt a message. We form a private key that satisfies the given formula and can use this to decrypt a message encrypted by the public key. We can release our public key to the world and people can encrypt messages to us using this key. We keep our private key secret and can use it to read those messages.

[raymondsecurityadventures]

Lecture 3

Risk Evaluation and the Folly of Mankind 

It’s not uncommon for low risk, high impact events to be grossly underestimated or grossly overestimated. It’s in human nature to think this way, as some events are so highly unlikely to occur that we never see it occur hence we don’t tend to think about them. And so, security features that protect against such events are often given less consideration than they should otherwise deserve.  On the flip side, threats that are relatively low impact (compared to say the human cost of drink driving) such as terrorism are very visible and the response by governments to such attacks are often very kneejerk-type reactions, with the world’s governments tripling defence spending since 9/11 and implementing incredibly tight airport security controls. This works to assuage our ‘relatively’ unfounded fear of acts of terror, fund the military industrial complex and provide an excuse to introduce repressive legislation that causes more harm to society than multiple 9/11 attacks.

Another example mentioned was the Challenger disaster, wherein the official investigations exploring the possible causes simply stated that it was a freak occurrence that the O ring failed and that it would never happen again. One Richard Feynman however, in following the chain of authority down to the lowest level engineers found that the NASA executives’ publicised probabilities of failure were totally incorrect and that each lower link in the chain of authority provided a higher estimate to the risk of failure than their superior.  This was explained as an example of the tendency for humans to underestimate low risk events, with each manager in the hierarchy exaggerating their inferior’s claims. 

And so Richard preaches that we shouldn’t follow in the footsteps of our governments and managers and when thinking in the scope of security engineering we should always seek to verify the necessity and resources of introducing risk countermeasures. 

Countering the effects of conflicting interest

Introduce as many third parties - as partial as possible and with opposing interests - to help observe any possible risks and contribute them to the risk register.  This will serve to minimise the effects of conflicting interest by setting parties, whose interests lie in opposite directions, to the task and assuming that both parties will act in their own self-interest and balance one another out. 

Compliance Culture 

Is quite useful in that it prevents stupid mistakes from occurring, however, can be dangerous when people assume that merely compliance is enough to prevent risks.  Instead, compliance to a policy should be merely the minimum standard for threat annulment. 

Dealing with Risk:

1. Devote resources and develop countermeasures 2. Eat it (forgot point 2 hehe) 3. Give it to someone else e.g. an insurance company  4. Take it when it’s unavoidable 

Centralisation and its Issues:

Centralisation is the process of consolidating all power of a structure under a single authority. This process, as mentioned in our discussion of the Bell LaPadua model, will have the issue of a single point of failure but will also be less subject to the constraints of bureaucracy and in general, the opinions of the masses. 

Work Factor and its role in preventing attacks: 

Much of cryptography breaks down to the asymmetric information problem and that an attacker would be required to do a prohibitive amount of work in order to break a cipher, while messengers A and B will enjoy access to information which allows them to decipher text far more quickly. 

Insider Attacks: 

Are considered far more effective than most forms of attack as they’re more insidious in nature, difficult to uncover and depending on the insider’s level of access, potentially more impactful. In fact, it is often only when other insiders that have been captured/caught reveal the identities of an organisations malicious insiders that, that these attacks are able to be prevented. 

However, they appear to be under-considered by many companies and other organisations of the world and Richard believes it is because many simply refuse to acknowledge that anyone working under them would be corruptible.

The Key Problem: 

A wants to talk to 10000 people, but to talk to 10000 people safely A will require 10,000 keys. A is struggling to manage 10,000 keys, when suddenly another 10,000 people want to join and suddenly A is swamped with more keys. Enter public key cryptography.

Public Key Cryptography

Fixes this problem by making everyone’s keys public, however, this public key is simply used to identify the actual private key required to decode the message. So there will not be 10,000 keys floating around that need to be managed, everyone just has their own public key and, depending on the system, either a list of keys. 

RSA 

1. Large Prime Number Generation: generate 2 large primes, p and q, preferably of size 1024

2. Multiply them to generate a large composite number, n. This is the foundation of RSA’s security, as composite numbers are difficult to be decomposed into ints prime factors

3. Calculate Euler’s totient (phi) which is simply (p-1) * (q-1)

4. Determine a public key, e, which is simply a prime between 3 and phi paired with n.

5. We determine the inverse of the public key which is the private key, d, with phi, using the Extended Euclidean algorithm or brute force. Meaning that e * d mod (phi) = 1. We pair d with n as well. 

To encrypt a message ‘m’, we convert it to a large number and calculate m^e mod n = c, where c is the cipher text. 

To decrypt it, we simply apply the same calculation but using the cipher text and the private key. 

[comparecheapssl]

RSA Algorithm: A Trusted Method for Encrypting and Securing Data

The RSA algorithm is a commonly used method for secure data transmission in the field of cryptography. It is a type of public-key encryption, which means that it uses two different keys for the encryption and decryption process: a public key and a private key. The public key is used to encrypt the data, while the private key is used to decrypt it.

What is the RSA algorithm?

The RSA algorithm is a powerful encryption method that is widely used to protect sensitive information. It is a type of public-key encryption, which means that it uses two different keys for the encryption and decryption process: a public key and a private key. The public key is used to encrypt the data, while the private key is used to decrypt it.

RSA was first introduced in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and since then it has become the de facto standard for secure data transmission. It is based on the mathematical properties of large prime numbers, making it one of the most secure encryption methods currently in use.

The RSA algorithm works by first generating two large prime numbers, p and q. These prime numbers are used to calculate a third value, n, which is the product of p and q. The value of n is used as the modulus for both the public and private keys.

Read about – Cheap Code Signing Certificate

Why is the RSA algorithm used?

The RSA algorithm is used for secure data transmission because it provides both confidentiality and authenticity. It uses a pair of public and private keys to encrypt and decrypt messages, ensuring that only the intended recipient can read the message and that the message has not been tampered with. It is widely used for secure communications such as email, file transfer, and VPNs, and for digital signatures, software protection, and secure online transactions.

How does the RSA algorithm work?

The RSA algorithm is a method for secure data transmission. It is widely used in electronic commerce and other communications. The algorithm is based on the mathematical properties of large prime numbers and the difficulty of factoring the product of two large prime numbers.

The basic steps of the RSA algorithm are:

Select two large prime numbers, p and q.

Compute n = pq, where n is used as the modulus for both the public and private keys.

Select a public exponent e, where 1 < e < φ(n) (φ is the Euler’s totient function) and e is relatively prime to φ(n).

Compute the private exponent d, where d = e^-1 mod φ(n).

The public key is the pair of values (n, e) and the private key is the pair of values (n, d).

To encrypt a message, the sender uses the recipient’s public key (n, e) and raises the message to the power of e (mod n). To decrypt the message, the recipient uses their private key (n, d) and raises the encrypted message to the power of d (mod n).

Read About – SSL Certificate

Because the encryption and decryption keys are related by the properties of large prime numbers and modular arithmetic, it is computationally infeasible to determine the private key based on knowledge of the public key. This ensures that only the intended recipient can decrypt the message.

Example of RSA encryption algorithm

Here is an example of how the RSA encryption algorithm can be used to encrypt a message:

Select two large prime numbers, p = 61 and q = 53.

Compute n = pq = 61 * 53 = 3233, which will be used as the modulus for both the public and private keys.

Compute φ(n) = (p-1)(q-1) = (61-1)(53-1) = 3120.

Select a public exponent e, such as e = 17. (e is relatively prime to φ(n) = 3120)

Compute the private exponent d, using the extended Euclidean algorithm. We find that d = 2753.

The public key is the pair of values (n, e) = (3233, 17) and the private key is the pair of values (n, d) = (3233, 2753).

Read more

[asktoppatpurgatory]

Man, must be pretty exhausting in purgatory. And boring. Do you guys do anything at all in there?

”Nothin’ much aside from each other- and you guys now.”

[cityinmars-blog]

We ask hard questions because so many of the problems worth solving in life are hard. If they were easy, someone else would have solved them before you got to them. This is why college classes at top-tier universities have tests on which nearly no one clears 70%, much less gets a perfect score. They’re training future researchers, and the whole point of research is to find and answer questions that have never been solved. You can’t learn how to do that without fighting with problems you can’t solve. If you are consistently getting every problem in a class correct, you shouldn’t be too happy—it means you aren’t learning efficiently enough. You need to find a harder class.

The problem with not being challenged sufficiently goes well beyond not learning math (or whatever) as quickly as you can. I think a lot of what we do at AoPS is preparing students for challenges well outside mathematics. The same sort of strategies that go into solving very difficult math problems can be used to tackle a great many problems. I believe we’re teaching students how to think, how to approach difficult problems, and that math happens to be the best way to do so for many people.

The first step in dealing with difficult problems is to accept and understand their importance. Don’t duck them. They will teach you a lot more than a worksheet full of easy problems. Brilliant “Aha!” moments almost always spring from minds cultivated by long periods of frustration. But without that frustration, those brilliant ideas never arise.

Here are a few strategies for dealing with hard problems, and the frustration that comes with them:

Do something. Yeah, the problem is hard. Yeah, you have no idea what to do to solve it. At some point you have to stop staring and start trying stuff. Most of it won’t work. Accept that a lot of your effort will appear to have been wasted. But there’s a chance that one of your stabs will hit something, and even if it doesn’t, the effort may prepare your mind for the winning idea when the time comes. We started developing an elementary school curriculum months and months before we had the idea that became Beast Academy. Our lead curriculum developer wrote 100–200 pages of content, dreaming up lots of different styles and approaches we might use. Not a one of those pages will be in the final work, but they spurred a great many ideas for content we will use. Perhaps more importantly, it prepared us so that when we finally hit upon the Beast Academy idea, we were confident enough to pursue it.

Simplify the problem. Try smaller numbers and special cases. Remove restrictions. Or add restrictions. Set your sights a little lower, then raise them once you tackle the simpler problem.

Reflect on successes. You’ve solved lots of problems. Some of them were even hard problems! How did you do it? Start with problems that are similar to the one you face, but even think about others that have nothing to do with your current problem. Think about the strategies you used to solve those problems, and you might stumble on the solution. A few months ago, I was playing around with some Project Euler problems, and I came upon a problem that (eventually) boiled down to generating integer solutions to c² = a² + b² + ab in an efficient manner. Number theory is not my strength, but my path to the solution was to recall first the method for generating Pythagorean triples. Then, I thought about how to generate that method, and then the path to the solution became clear. (I’m guessing some of our more mathematically advanced readers have so internalized the solution process for this type of Diophantine equation that you don’t have to travel with Pythagoras to get there!)

Focus on what you haven’t used yet. Many problems (particularly geometry problems) have a lot of moving parts. Look back at the problem, and the discoveries you have made so far and ask yourself “What haven’t I used yet in any constructive way?” The answer to that question is often the key to your next step.

Work backwards. This is particularly useful when trying to discover proofs. Instead of starting from what you know and working towards what you want, start from what you want, and ask yourself what you need to get there.

Ask for help. This is hard for many outstanding students. You’re so used to getting everything right, to being the one everyone else asks, that it’s hard to admit you need help. When I first got to MOP my sophomore year, I was in way over my head. I understood very little of anything that happened in class. I asked for help from the professor once—it was very hard to get up the courage to do so. I didn’t understand anything he told me during the 15 minutes he worked privately with me. I just couldn’t admit it and ask for more help, so I stopped asking. I could have learned much, much more had I just been more willing to admit to people that I just didn’t understand. (This is part of why our classes now have a feature that allows students to ask questions anonymously.) Get over it. You will get stuck. You will need help. And if you ask for it, you’ll get much farther than if you don’t.

Start early. This doesn’t help much with timed tests, but with the longer-range assignments that are parts of college and of life, it’s essential. Don’t wait until the last minute—hard problems are hard enough without having to deal with time pressure. Moreover, complex ideas take a long time to understand fully. The people you know who seem wicked smart, and who seem to come up with ideas much faster than you possibly could, are often people who have simply thought about the issues for much longer than you have. I used this strategy throughout college to great success—in the first few weeks of each semester, I worked far ahead in all of my classes. Therefore, by the end of the semester, I had been thinking about the key ideas for a lot longer than most of my classmates, making the exams and such at the end of the course a lot easier.

Take a break. Get away from the problem for a bit. When you come back to it, you may find that you haven’t entirely gotten away from the problem at all—the background processes of your brain have continued plugging away, and you’ll find yourself a lot closer to the solution. Of course, it’s a lot easier to take a break if you start early.

Start over. Put all your earlier work aside, get a fresh sheet of paper, and try to start from scratch. Your other work will still be there if you want to draw from it later, and it may have prepared you to take advantage of insights you make in your second go-round.

Give up. You won’t solve them all. At some point, it’s time to cut your losses and move on. This is especially true when you’re in training, and trying to learn new things. A single difficult problem is usually going to teach you more in the first hour or two than it will in the next six, and there are a lot more problems to learn from. So, set yourself a time limit, and if you’re still hopelessly stuck at the end of it, then read the solutions and move on.

Be introspective. If you do give up and read the solution, then read it actively, not passively. As you read it, think about what clues in the problem could have led you to this solution. Think about what you did wrong in your investigation. If there are math facts in the solution that you don’t understand, then go investigate. I was completely befuddled the first time I saw a bunch of stuff about “mod”s in an olympiad solution—we didn’t have the internet then, so I couldn’t easily find out how straightforward modular arithmetic is! You have the internet now, so you have no excuse. If you did solve the problem, don’t just pat yourself on the back. Think about the key steps you made, and what the signs were to try them. Think about the blind alleys you explored en route to the solution, and how you could have avoided them. Those lessons will serve you well later.

Come back. If you gave up and looked at the solutions, then come back and try the problem again a few weeks later. If you don’t have any solutions to look at, keep the problem alive. Store it away on paper or in your mind. Richard Feynman once wrote that he would keep four or five problems active in the back of his mind. Whenever he heard a new strategy or technique, he would quickly run through his problems and see if he could use it to solve one of his problems. He credits this practice for some of the anecdotes that gave Feynman such a reputation for being a genius. It’s further evidence that being a genius is an awful lot about effort, preparation, and being comfortable with challenges.

[mobius-warzone-cheats-fj]

mobius warzone cheats

⭐ ⏩⏩⏩️ DOWNLOAD MOD - LINK 🔥🔥🔥🔥🔥 #moonryde #bblade #warzone #warzoneclip #soloyolo #perte #neiperte #foryou #fnatic #warzonecheat #warzonecheater #pow3rtv #cheat. Genshin Impact Barbara Hangout Event Memories: How to Unlock All the Endings · Gate of Mobius-Leitfaden: Tipps, Cheats und Strategien · Guia Gate of Mobius: dicas. corner discover race cheat t amazon differently egg shake silly location euler garuda invertebrate landmass licht miroslav mobius rosita thun bild. /package/nuget/Final-Fantasy-Mobiusmobile-hack-Magicite-mod-apk. Call of Duty: Warzone Guide - Guía de misiones del "equipo perdido" Noticias Fin del juego para Mobius Final Fantasy. the bureau xcom declassified cheat engine halo 5 new warzone map mobius final fantasy apksplinter cell chaos theory patchusb halo 5 warzone bosses mobius final fantasy download. +orphan +cheat +endowed +sadness +chairperson +tipperary +southbound +std +spearheading +lun +slavia +mobius +sympathize +psychedelics +blouse +ait. costa hairy chest cheat codes for ps2 bmx xxx. adult website mobius strip puzzle. cod-warzone-cheats dice. Se anuncia Call of Duty Warzone: Anti-cheats. Activision anunció que Call of Duty: El DLC del título de Mobius Digital estará disponible este año.

[muggle-writes]

Rules: Answer 21 questions and then tag 21 people who you want to get to know better.

tagged by @elizabethsyson

Nickname: Muggle is my nickname, but when I went by Muggle in person for more than a month at a time, it naturally got abbreviated, usually to Mugz

Zodiac: Aquarius

Last movie I saw: into the spiderverse (same answer as last time. I don't watch that many movies tbh except around Christmas. unless YouTube counts in which case... music of some sort? idk links for the next answer)

Favorite musician: changes by the day. I've kinda been in an acapella and/or folk music mood recently so the Maccabeats and Peter Hollens are in my YouTube and Spotify history a lot recently. also I'm eternally in awe of Forte Handbell Quartet (eta a longer video; i recommend skipping to the techno piece or the Jurassic Park theme)

Last thing I googled: "vine why are you buying clothes at the soup store" (my wife hasn't seen it; also i can't find the vine because apparently it's a much bigger meme than I realized). before that it was "chgrp not root" because work and group permissions are useful when they work

Song stuck in my head: well for most of the day when I haven't been actively listening to something, it's been the Pokemon RSE route-walking music. (but that somehow happens frequently when I'm in the no-music-no-internet room at work, as I was for most of the day, and I don't know how I accidentally trained my brain to make that connection). right now, surprisingly, I don't have any background music playing in my head. I think it's because the humidifier provides just enough white noise that my brain doesn't feel the need to provide its own

Other blogs: my main is @muggle-the-hat and I'm a mod on @why-do-neurotypicals but we've gotten one ask ever so that blog has been dormant for a while. I have a bunch of other sideblogs, but they're all small and I use different screen names on each of them (enby life: no idea which name suits me best so I may as well try them out) so i feel like it would just confuse things to link them.

Following: blogs matching all the themes of my sideblogs, (including this one, which is writeblr), korean langblr, jumblr, assorted fandom blogs, authors of my more favorite fanfictions (some overlap with other categories), and irl friends and acquaintances (including one fandom blog turned irl friend)

Do I get asks: on my main if at all, which isn't really surprising because i have hundreds of followers there and maybe 60 followers combined among the rest. but I get asks far less often than I reblog ask memes so... I'm always happy to get more. I do get tagged in ask games more on this one, but writeblr is actually vaguely organized about tag lists so that makes sense. also I used to get tagged a bunch on my main and I rarely could find the posts again to follow up when I had time to answer.

What I’m Wearing: pajamas. staying warm and cozy

Lucky number: I don't remember what I said last time, but I like a lot of numbers. 64 is a good number. recently I've been debugging software in which 0x3E is my lucky status number and 0x0E taunts me. (um, decimal 62 and 14). Also my other favorite number i can't share until it's no longer the combination to the lock to the Secret Room. (or realistically never because opsec and i shouldn't make public the types of parents we use for that combination lock), honestly I aim to be like.... ah, I'm sure the anecdote involves G.H. Hardy but i don't remember on which side. anyway one mathematician remarked to another about how the id number of the taxi he rode in was sadly uninteresting, and the one I aspire to be like, argued "what are you talking about, this number is interesting because ______" and I'd like to be able to do that for any arbitrary number thrown at me. (hi yes math is good, history is hard, math history is interesting yet i still forget the people even if i remember the math. except when things are named after people, but that tends to be, like, Euler and LaGrange and other people who did lots of cool science things so i remember the methods and the names of the methods separately which never helps)

Amount of sleep: ....depression both screws with my sleep schedule and means I always feel like I need more sleep except when I wake up at 5pm and feel like I've wasted the day. so yeah. I can never get enough sleep

Favorite food: yes (why do I have to pick a favorite?) uh, chocolate in most forms, many other sweet things, red meats (especially if served with potatoes), curry (especially if it has "too much" ginger), fresh-baked bread, chai the way my favorite local Indian restaurant makes it (spicier with just a little bit of sweet, which is the opposite of what i can get from the mocha machine at work which is wayyy sweet with a hint of spice but that inferior chai is still superior to coffee so i drink too much of it). also vegetables which I really don't eat enough of: sauteed zucchini and onions, roasted broccoli

Dream trip: dreaming requires creativity and tbh I funnel that mostly into my writing instead. I wouldn't mind going back to Korea for another visit though

Dream job: my current job is pretty good when I feel productive and when my debugging tools actually produce data maybe??? (they were not being helpful today. but i still mostly like my job.) dream job is probably this but with seniority and confidence and double the salary (while living in a similar area of the country; I wouldn't want to double my salary by moving to work for Google in California and having less available after rent than I do now)

Describe yourself as aesthetic things:

the smell of old books

the first glow of sunrise (the sunrise painting the mountains pink and gold)

a rainbow in the spray from a waterfall

the flicker of distant lightning (watching a thunderstorm fade into the distance)

this picture

Random fact: about me or about the world?

how about a combination answer: when we got our new handbell music this season, we only looked at half the pieces our first rehearsal and afterwards I tried to look up one of the pieces we hadn't gotten to on YouTube because it's got a weird time signature and I wanted to get a feel for how fast it would go and how strict the counting is...... except it turns out we're the first group to ever play the piece. it was commissioned recently but seeing my conductor's name on the page didn't tell me how new it was because he's super prolific. (the fact that it was on printer paper without the publisher's graphics should have been a giveaway but it's only the second time I've been among the first to play one of his pieces so I think I can be excused for not realizing)

Languages: mostly just English, but I took Spanish for years, so I can hold simple conversations in it. I can almost read sound out Hebrew fast enough to keep up in services, and I know some random Hebrew vocab but comparatively no grammar. and I took Korean in college, enough that I can recognize sentence structure but I can really only speak tourist-Korean, though I can sound anything out (if it's typed. handwriting is hit or miss.) in both Hebrew and Korean (and Spanish tbh but i don't often listen to Spanish music) I'm very proud when I can separate the words enough, listening to a song, to translate them without looking up the lyrics. also I tried to learn Japanese from Duolingo when it was new, but I still hadn't gotten the kana straight when it started progressing to kanji so that was a rough time and I went back to Hebrew.

tbh I "dabble" in "language learning" which really means I start a million courses on Duo and stick with none of them. with the notable exception of French, which I acknowledge is super common and probably a good idea to learn but the spelling and pronunciation seem so arbitrary I'm scared to look close enough to learn it properly, and I've never particularly considered starting the Duolingo course for French

I think I lost a few questions, because that's only 18 answers. whoops.

um... who to tag

@abluescarfonwaston if school hasn't drowned you in work yet and @copperscales I'm interested in both of your choices for lucky numbers especially.

... wow I'm blanking on other mutuals I haven't tagged recently. as usual lmk if you'd like to be edited in, or just answer the questions and tag me back, that's great too.

[quizllc]

aΦ(h1)≡ 1 (mod m) is called:

aΦ(h1)≡ 1 (mod m) is called:

A. Euclid Theorem B. Fermit Theorem C. Euler’s Theorem D. Hensel Lemma

[comp6841]

The RSA Algorithm

Step 1: Picking Primes

The first step requires to choose two sufficiently large primes p and q - in practice these are usually 2048 bits, however 4096 bits would be on the safer side. I’m going to ignore the methods of secure random number generation here and assume that we are able to generate numbers of these length with sufficiently large entropy. Now we just have to check that each of the numbers we generate is a prime - if we have a look at the prime number theorem we’ll see that given a 4096 bit number we get the following:

So basically on average you will need to check 3076 numbers which are 4096 bits (assuming the most significant is always 1) before you find a prime. If you do the calculations but don’t make the assumption that the most significant bit is 1, you get a slightly higher percent approximation (around 0.035%ish) however this is only rough work here. To do this we usually utilise the Miller-Rabin test on p which involves the following:

Write p in the form p = 2^s*q+1 for some odd q

Pick an integer a in the range [2, p-1]

Calculate x = a^q (mod p)

If x = 1 or x = p - 1 then we say it is “probably prime”

Check a^(2^i) (mod n) = -1 for each integer i in the range [0, s-1]

If we can find such an i, then we say it is “probably prime”

If we get to the end here, then p is “composite”

By applying the Miller-Rabin test multiple times we can significantly reduce the probability - it turns out that the probability a composite number will pass the test is at most 1/4. So if we do 8 passes of Miller-Rabin then there is a maximum probability that it will actually be composite of 1/65536 - this would easily be sufficiently small enough for our purposes. The reason this is sufficient is because it is almost certain that the process of RSA will fail, if it is not prime, in decryption - this is because the algorithm is essentially a powerful primality test. I should probably mention as a sidenote that Miller-Rabin doesn’t detect Carmichael numbers:

Carmichael numbers satisfy the above property for all integers b coprime to n. These numbers can affect the security in RSA as some of their factors are relatively smaller - remember that the security in RSA rests on the fact that they are hard to factor. It’s important to note that they are relatively rare.

Specific Example: we will use the small primes 17 and 31 to demonstrate the algorithm.

Step 2: Calculate the value of n

Calculate n = p * q - this will be used as the modulus for the keys and will be available as part of the public key.

Specific Example: calculate n = 17 * 31 = 527

Step 3: Determine Euler’s totient function

We need to calculate Euler’s quotient ϕ(n)   = (p - 1) * (q - 1). This represents the number of positive integers that are relatively prime up to our integer n.

Specific Example: ϕ (n) = (17 - 1) * (31 - 1) = 480

Step 4: Calculate the encryption key e

In this part we need to find a number e that is coprime with ϕ(n) - this means that it doesn’t share any factors in the range [3,  ϕ(n)]. Interestingly enough, Fermat primes  (99% of the time) are almost always chosen for this such as 3, 5, 17, 257 and 65537. The reason being for this is that it is of the form F_n = 2^(2^n)+1 and as a result makes the calculations run a lot faster (without much of a significant setback in security). There are some attacks based on the Coppersmith Theorem available for using small values such as 3 as the encryption key, however they are far from a total break in security - paper on it here.

Specific Example: we will take the largest Fermat prime e = 257 in this case - this means our public key is the pairing (e = 257, n = 527)

Step 5: Determine the decryption key d

To find the decryption key we need to solve the equation d * e (mod ϕ) = 1, where d is the decryption key. We can utilise the Extended Euclidean algorithm to do this.

Specific example: we need to solve the equation d * 257 (mod 480) = 1 - we will do this via the Extended Euclidean Algorithm

So a solution to this equation is if we take d = 353. This means our private key pair is (d = 353, n = 527)

Step 6: Encrypting with the public key

The first thing we must do is convert the message into integer form - in the case of characters in a message we can just use their ASCII codes. Given a plaintext message m, we can then determine the ciphertext c with the formula c = m ^ e (mod n).

Specific Example: if we wanted to encrypt the letter ‘A’ then we would use the ASCII code of 65. So the ciphertext would be c = 65 ^ 257 (mod 527) = 456

Step 7: Decrypting with the private key

We convert the cipher text into an integer (if it isn’t already) then can determine the plaintext m = c ^ d (mod n). The reason this relationship works is due to the fact that (m^e)^d = m (mod n) - you can prove this result using either Fermat’s little theorem or Euler’s theorem (see here for proof).

Specific Example: we calculate the plaintext m = 456 ^ 353 (mod 527) = 65. This represents the letter ‘A’ in ASCII so we got our original result back